Dévelopements limités#
Une méthode usuelle pour étudier des fonctions et de les approcher par des fonctions plus simples. Les fonctions polynômes forment une classe de fonctions élémentaires qui se manipulent facilement vis à vis des opérations usuelles (dérivation, somme, produit, intégration, dérivation,…). Ainsi, il est naturel d’essayer d’approcher les fonctions par des polynômes.
Les développements limités correspondent à une mise en oeuvre locale de ce programme. Chercher un développement limité d’une fonction \(f\) au voisinage d’un point \(a\), c’est chercher un polynôme qui, au voisinage de \(a\), se comporte comme \(f\). Voici un site qui donne le dévelopement limité d’une fonction. Voici un site qui donne la courbe d’une fonction et la courbe du polynôme de son développement limité.
Définition
Soit \(f : I \to \mathbb R\) une fonction et soit \(a \in I\) . Soit \(n \in \mathbb N\), on dit que \(f\) admet un développement limité d’ordre n en a (ou un \(DL_n(a)\)) lorsqu’il existe un polynôme \(T\) de degré au plus \(n\) tel que :
Si c’est le cas, alors le polynôme \(T(x − a)\) est appelé partie régulière et la partie \(\underset{a}{o}((x − a)^n)\) est appelé reste du \(DL_n(a)\).
Exemple
On a \(\sin x \underset{0}{\sim} x\) donc par définition \(\sin x = x + \underset{0}{o}(x)\). C’est un \(DL_1(0)\) de \(\sin x\).
Formule de Taylor#
Théorème(Théorème de Taylor-Young)
Soit \(f : I\rightarrow\mathbb{R}\) une fonction de classe \(\mathscr{C}^{n},\,(n\in\mathbb{N},\) et soit \(a\in I.\) Alors pour tout \(x\in I\) on a:
avec \(\varepsilon(x)\rightarrow0\) quand \(x\rightarrow a.\)
On peut aussi écrire:
Exercice
Soit \(f :]-1,+\infty[\rightarrow \mathbb{R}\) définit par \(f(x) = \ln(1+x)\).
On a \(f\) est infiniment dérivable. Appliquons la formule de Taylor-Young à la fonction \(f\) au voisinage de \(0,\) soit \(T_n\) la fonction polynômiale associée à chaque \(n,\) pour cela on calcule d’abord \(f^{(k)}(0)\) pour \(k=0,1,\ldots,n.\)
\(f(0)=0\)
\(f'(0)=1\)
\(f''(0)=-1\)
\(f^{(3)}(0)=2,\ldots\)
Montrer par récurrence que \(f^{(n)}(x)=(-1)^{n-1}(n-1)!\frac{1}{(1+x)^n}\) et alors \(f^{(n)}(0)=(-1)^{n-1}(n-1)!\)
Voici donc les premiers polynômes de Taylor:
Les formules de Taylor nous disent que les restes sont de plus en plus petits lorsque \(n\) croît. Sur le dessins les graphes des polynômes \(T_0,\,T_1,\,T_2,\,T_3\) s’approchent de plus en plus du graphe de \(f.\) Attention ceci n’est vrai qu’autour de \(0.\)
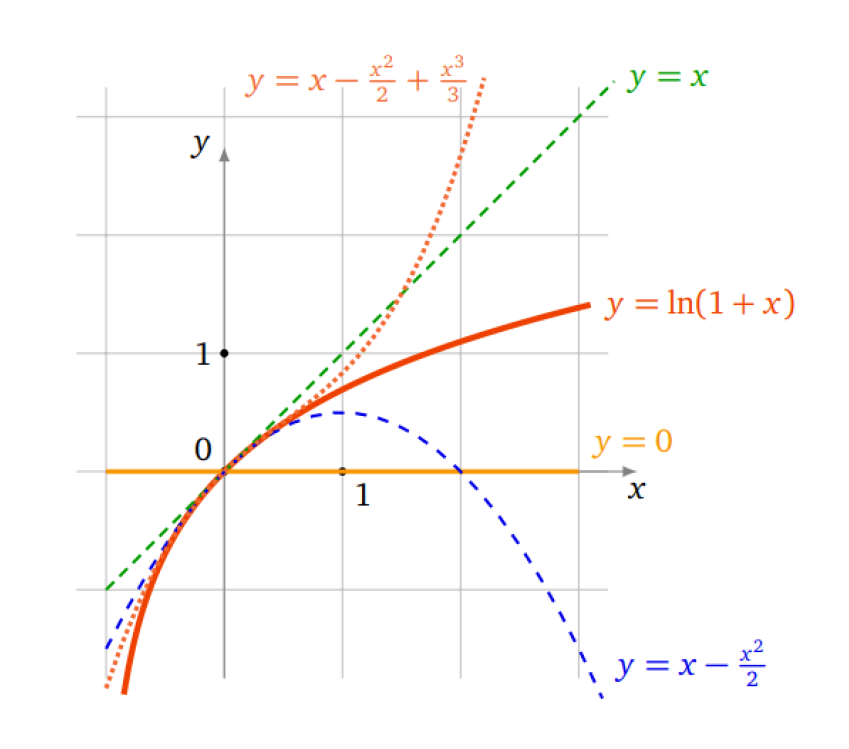
Fig. 4 Approximation#
Cas particulier : Formule de Taylor-Young au voisinage de 0. On se ramène souvent au cas particulier où \(a=0\)
avec \(\varepsilon(x)\rightarrow0\) quand \(x\rightarrow .\)
On écrit souvent cette formule avec la notation dite “petit \(o\)”
Développements limités au voisinage d’un point#
Définition et existence#
Soit \(I\) un intervalle ouvert et \(f :I\rightarrow\mathbb{R}\) une fonction quelconque.
Definition
Pour \(a\in I\) et \(n\in\mathbb{N},\) on dit que \(f\) admet un développement limité (DL) au point \(a\) et à l’ordre \(n,\) s’il existe des réels \(c_0,c_1,\ldots,c_n\) et une fonction \(\varepsilon:I\rightarrow\mathbb{R}\) telle que \(\lim\limits_{\substack{x \rightarrow a}}\varepsilon(x)=0\) de sorte que pour tout \(x\in I:\)
L’égalité précédente s’appelle un DL de \(f\) au voisinage de \(a\) à l’ordre \(n.\)
Le terme \(c_0+c_1(x-a)+c_2(x-a)^2+\ldots+c_n(x-a)^n\) est appelé la partie polynomiale du DL.
Le terme \((x-a)^n \varepsilon(x)\) est appelé le reste du DL.
La formule de Taylor-Young permet d’obtenir immédiatement des développements limités en posant \(c_k=\frac{f^{(k)}}{k!}.\)
Remarque
Si \(f\) est de classe \(\mathscr{C}^{n}\) au voisinage d’un point \(0,\) un DL en \(0\) à l’ordre \(n\) est l’expression:
\[ f(x)=f(0)+f'(0)x+\frac{f''(0)}{2!}x^2+\ldots+\frac{f^{(n)}(0)}{n!}x^n+x^n \varepsilon(x) \]Si \(f\) admet un DL en un point \(a\) à l’ordre \(n\) alors elle en possède un pour tout \(k\leq n.\) En effet
\[\begin{eqnarray*} f(x)&=& f(a)+f'(a)(x-a)+\frac{f''(a)}{2!}(x-a)^2+\ldots+\frac{f^{(k)}(a)}{k!}(x-a)^k\\ && +\frac{f^{(k+1)}(a)}{(k+1)!}(x-a)^{k+1}+\ldots+\frac{f^{(n)}(a)}{n!}(x-a)^n+(x-a)^n \varepsilon(x) \end{eqnarray*}\]
Unicité#
Proposition
Si \(f\) admet un \(DL\) alors ce \(DL\) est unique.
Preuve: En exercice (supposer l’existence de deux DL, puis utiliser la propriété d’un polynôme nul.)
Corollaire
Si \(f\) est paire (resp. impaire) alors la partie polynomiale de son \(DL\) en \(0\) ne contient que des monômes de degrés pairs (resp. impairs).
Remarque
Si \(f\) admet un \(DL\) en un point \(a\) à l’ordre \(n\geq1,\) alors \(f\) est dérivable en \(a\) et on a \(c_0 = f(a)\) et \(c_1 = f'(a).\) Par conséquent \(y = c_0 + c_1(x-a)\) est l’équation de la tangente au graphe de \(f\) au point d’abscisse \(a.\)
DL des fonctions usuelles à l’origine#
Les DL suivants en \(0\) proviennent de la formule de Taylor-Young.
\(\exp x=1+\frac{x}{1!}+\frac{x^2}{2!}+\ldots+\frac{x^n}{n!}+x^n \varepsilon(x)\)
\(chx=1+\frac{x^2}{2!}+\frac{x^4}{4!}\ldots+\frac{x^{2n}}{(2n)!}+x^{2n+1} \varepsilon(x)\)
\(shx=1+\frac{x}{1!}\frac{x^3}{3!}+\frac{x^5}{5!}\ldots+\frac{x^{2n+1}}{(2n+1)!}+x^{2n+2} \varepsilon(x)\)
\(\cos x=1-\frac{x^2}{2!}+\frac{x^4}{4!}\ldots+(-1)^n\frac{x^{2n}}{(2n)!}+x^{2n+1} \varepsilon(x)\)
\(shx=1+\frac{x}{1!}\frac{x^3}{3!}+\frac{x^5}{5!}\ldots+(-1)^n\frac{x^{2n+1}}{(2n+1)!}+x^{2n+2} \varepsilon(x)\)
\(\frac{1}{1-x}=1+x+x^2+\ldots+x^n+x^n \varepsilon(x)\)
\(\frac{1}{1+x}=1-x+x^2-x^3+\ldots+(-1)^n x^n+x^n \varepsilon(x)\)
\(\ln(1+x)=x-\frac{x^2}{2}+\frac{x^3}{3}-\ldots+(-1)^{n-1} \frac{x^n}{n}+x^n \varepsilon(x)\)
Généralement, pour \(\alpha\neq -1,\) on a:
\((1+x)^{\alpha}=1+\alpha x+\frac{\alpha(\alpha-1)}{2}x^2+\ldots+\frac{\alpha(\alpha-1)\ldots(\alpha-n+1)}{n!}x^n+x^{n} \varepsilon(x)\)
En particulier, pour \(\alpha=\frac{1}{2},\) on a:
\(\sqrt{1+x}=1+\frac{x}{2}-\frac{1}{8}x^2+\ldots+(-1)^n\frac{1.3.5\ldots.(2n-3)}{2^n n!}x^n+x^n \varepsilon(x)\)
\(DL\) des fonctions en un point quelconque#
La fonction \(f\) admet un \(DL\) au voisinage d’un point \(a\) si et seulement si la fonction \(x\mapsto f(x+a)\) admet un \(DL\) au voisinage de \(0.\) Souvent on ramène donc le problème en \(0\) en faisant le changement de variables \(h=x-a.\)
Exercice
\(DL\) de \(f(x)=\exp x\) en \(1.\)
On pose \(h=x-1.\) Si \(x\) est proche de \(1\) alors \(h\) est proche de \(0.\) Nous allons nous ramener à un \(DL\) de \(\exp h\) en \(h = 0.\) On note \(e = \exp 1.\)
où \(\lim\limits_{\substack{x \rightarrow 1}}\varepsilon(x-1)=0\)
Opérations sur les développements limités#
Somme et produit#
On suppose que \(f\) et \(g\) sont deux fonctions qui admettent des \(DL\) en \(0\) à l’ordre \(n:\)
Proposition
\(f+g\) admet un \(DL\) en \(0\) l’ordre \(n\) qui est:
\[\begin{eqnarray*} (f+g)(x) &=& f(x)+g(x)\\ &=& (c_0+d_0)+(c_1+d_1)x+(c_0+d_0)x^2+\ldots+(c_n+d_n) x^n +x^{n}\varepsilon(x) \end{eqnarray*}\]\(f\times g\) admet un \(DL\) en \(0\) l’ordre \(n\) qui est:
\[\begin{eqnarray*} (f\times g)(x) &=& f(x)\times g(x)\\ &=& T_n(x)+x^n \varepsilon(x) \end{eqnarray*}\]où \(T_n(x)\) est le polynôme \((c_0+c_1 x+\ldots+c_n x^n)\times (d_0+d_1 x+\ldots+d_n x^n)\) tronqué à l’ordre \(n.\)
Exercice
Calculer le \(DL\) de \(\cos x \times\sqrt{1+x}\) à l’ordre \(2,\)
On a \(\cos x= 1-\frac{x^2}{2}+x^2 \varepsilon_1 (x)\) et \(\sqrt{1+x}=1+\frac{1}{2}x-\frac{1}{8}x^2+x^2\varepsilon_2 (x).\)
Donc:
Composition#
Soient \(f(x)=C(x)+x^n \varepsilon_1 (x)=c_0+c_1 x+\ldots+c_n x^n +x^n \varepsilon_1 (x)\) et \(g(x)=D(x)+x^n \varepsilon_2 (x)=d_0+d_1 x+\ldots+d_n x^n +x^n \varepsilon_2 (x)\)
Proposition
Si \(g(0) = 0\) (c’est-à-dire \(d_0 = 0\)) alors la fonction \(f\circ g\) admet un \(DL\) en \(0\) à l’ordre \(n\) dont la partie polynomiale est le polynôme tronqué à l’ordre \(n\) de la composition \(C(D(x)).\)
Exercice
Soit \(h(x)=\sqrt{\cos x},\) On cherche le \(DL\) de \(h\) en \(0\) à l’ordre \(4.\) On pose \(f(u)=\sqrt{1+u},\) alors on a \(f(u)=1+\frac{1}{2}u-\frac{1}{8}u^2+u^2\varepsilon (u)\) au voisinage de \(0\) à l’ordre \(2,\) et si on pose \(u(x)=\cos x-1,\) alors \(h(x)=f(u(x)),\) et \(u(0)=0,\) D’autre part le \(DL\) de \(u(x)\) en \(x = 0\) à l’ordre \(4\) est: \(u=-\frac{1}{2}x^2+\frac{1}{24}x^4+x^4 \varepsilon(x),\) en appliquant la prop .., on a \(u^2=\frac{1}{4}x^4+x^4 \varepsilon(x).\) D’où,
Division#
Soit à déterminer le DL de \(f/g,\) quitte à multiplier le DL de \(f\) par celui de \(1/g,\) il suffier de trouver le DL de ce dernier,
en posant \(f(x)=c_0+c_1 x+\ldots+c_n x^n +x^n \varepsilon_1 (x)\quad\mbox{et}\quad g(x)=d_0+d_1 x+\ldots+d_n x^n +x^n \varepsilon_2 (x)\)
cherchons le DL de \(1/g,\) pour cela on utilise le DL de \(\frac{1}{1+u},\)
Si \(d_0=1,\) \(u=d_1 x+\ldots+d_n x^n +x^n \varepsilon(x),\)
Si \(d_0\) est quelconque avec \(d_0 \neq0\) alors on se ramène au cas précédent en écrivant
\(\frac{1}{g(x)}=\frac{1}{d_0}\frac{1}{1+\frac{d_1}{d_0}x+\ldots+\frac{d_n}{d_0}x^n+\frac{x^n \varepsilon_2 (x)}{d_0}}\)
Si \(d_0 = 0\) alors on factorise par \(x^k\) (pour un certain \(k\)) afin de se ramener aux cas précédents.
Exercice
DL de \(\frac{1+x}{2+x}\) en \(0\) à l’ordre \(4.\)
Applications des développements limités, Calculs de limites#
Les DL sont très efficaces pour calculer des limites ayant des formes indéterminées ! Il suffit juste de remarquer que si \(f(x)=c_0+c_1 (x-a)+\ldots\) alors \(\lim\limits_{\substack{x \rightarrow a}}f(x)=c_0\)
Limite en \(0\) de \(\frac{\ln(1+x)-\tan x+\frac{1}{2}\sin^2 x}{3 x^2 \sin^2 x}\)
Notons \(\frac{f(x)}{g(x)}\) cette fraction.
En \(0,\)
Ainsi \(\frac{f(x)}{g(x)}=\frac{-\frac{5}{12}x^4+o(x^4)}{3x^4+o(x^4)}=\frac{-\frac{5}{12}+o(1)}{3+o(1)}.\)
D’où,
