Fonctions circulaires inverses#
Arccosinus#
Considérons la fonction cosinus \(\cos : \mathbb{R}\rightarrow[−1,1], x \mapsto\cos x.\) Pour obtenir une bijection à partir de cette fonction, il faut considérer la restriction de cosinus à l’intervalle \([0,\pi].\) Sur cet intervalle la fonction cosinus est continue et strictement décroissante, donc la restriction
est une bijection. Sa bijection réciproque est la fonction arccosinus:
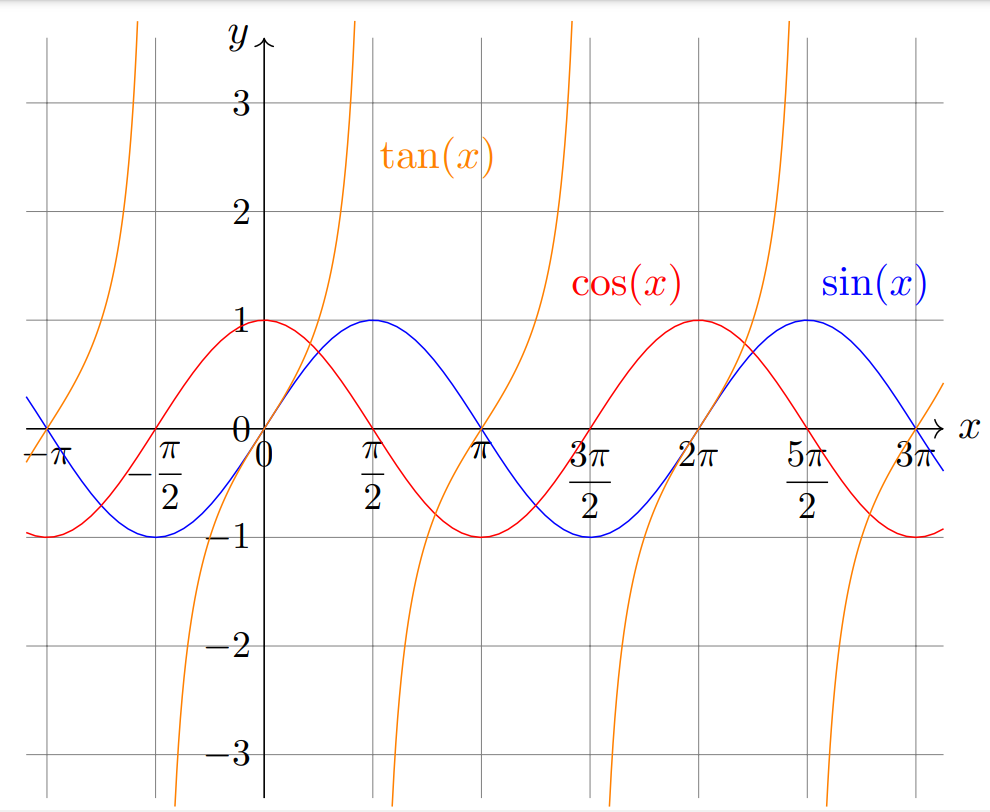
Fig. 1 fonctions sin cos et leurs inverse#
On a donc, par définition de la bijection réciproque:
Autrement dit:
Notons finalement que la fonction arccosinus est dérivable sur l’intervalle \(]-1,1[\) et
Démonstration:
On a l’égalité \(\cos(\arccos x) = x\) que l’on dérive :
Arcsinus#
La restriction
est une bijection. Sa bijection réciproque est la fonction arcsinus définie par
On a alors: \(\forall x\in[-\frac{\pi}{2},\frac{\pi}{2}] , \sin (x)=y\Leftrightarrow x=\arcsin(y).\)
La fonction arcsinus est dérivable sur l’intervalle \(]-1,1[\) et
Arctangente#
La restriction \(\tan:]-\frac{\pi}{2},\frac{\pi}{2}[\rightarrow\mathbb{R}\) est une bijection. Sa bijection réciproque est la fonction arctangente:
Ainsi
Et si \(x\in ]-\frac{\pi}{2},\frac{\pi}{2}[,\) alors \(\tan(x)=y\Leftrightarrow x=\arctan y.\)
Fonctions hyperboliques et hyperboliques inverses#
Cosinus hyperbolique et son inverse#
Pour \(x\in \mathbb{R},\) le cosinus hyperbolique est :
La restriction \(ch: [0,+\infty[\rightarrow[1,+\infty[\) est une bijection. Sa bijection réciproque est \(argch:[1,+\infty[\rightarrow[0,+\infty[\)
Sinus hyperbolique et son inverse#
Pour \(x\in \mathbb{R},\) le sinus hyperbolique est:
\(sh:\mathbb{R}\rightarrow\mathbb{R}\) est une fonction continue, dérivable, strictement croissante vérifiant \(\lim\limits_{\substack{x\rightarrow-\infty}}shx=-\infty\) et \(\lim\limits_{\substack{x\rightarrow+\infty}}shx=+\infty,\) c’est donc une bijection. Sa bijection réciproque est \(argsh:\mathbb{R}\rightarrow \mathbb{R}.\)
Proposition
\(ch^2 x - sh^2 x=1.\)
\(ch'x = shx, \;sh'x = chx.\)
argsh est dérivable et \(argsh'x=\frac{1}{\sqrt{x^2+1}}\)
\(argshx = \ln(x+\sqrt{x^2 +1}).\)
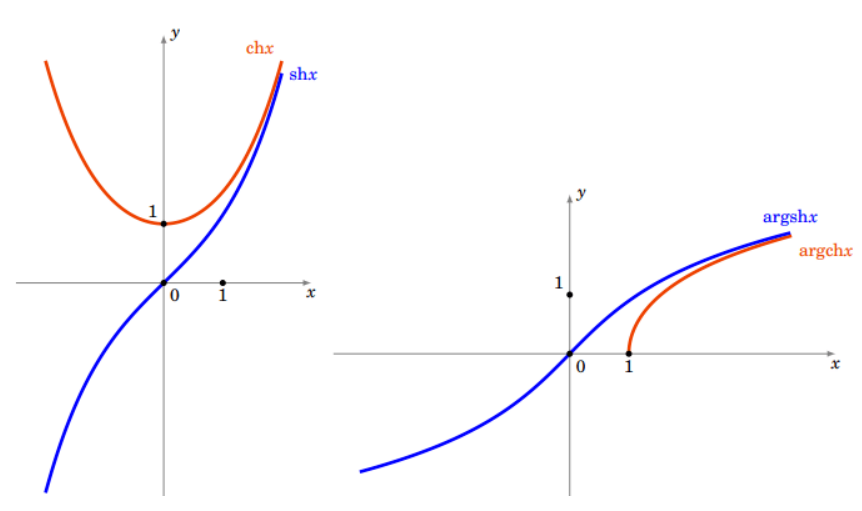
Fig. 2 fonctions sh, ch, argch et argsh#
Tangente hyperbolique et son inverse#
Par définition la tangente hyperbolique est :
La fonction \(th :\mathbb{R}\rightarrow]-1,1[\) est une bijection, on note \(argth :]-1,1[\rightarrow\mathbb{R}\) sa bijection réciproque.
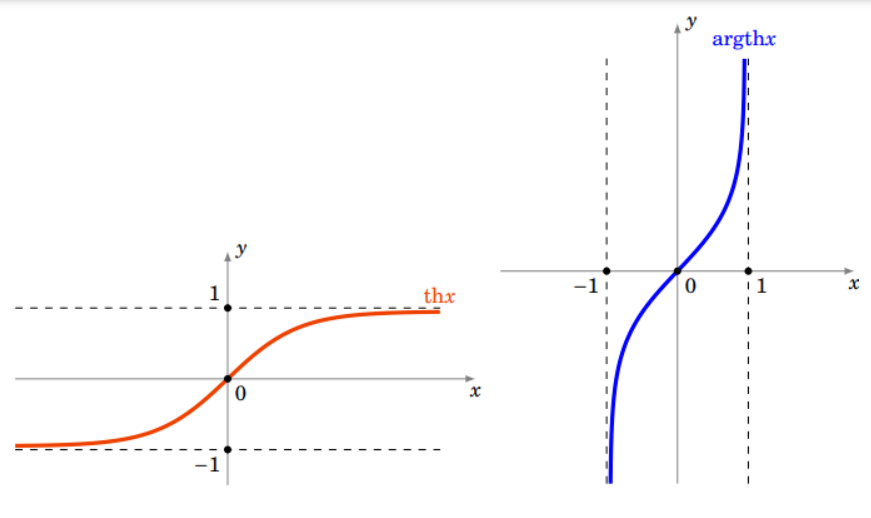
Fig. 3 fonctions th et argth#
Trigonométrie hyperbolique#
Dérivées de fonctions hyperboliques et leurs inverses
formules trigonometriques#
Rapel:#
les fonctions \(\sin\) et \(\cos\) sont definies sur \(\mathbb{R}\) et a valeurs dans \([-1, 1]\), \(2\pi\)-periodiques.
La fonction \(\tan\) est definie sur \(\mathbb{R}\setminus \{\frac{\pi}{2} +k\pi, k\in \mathbb{Z}\) a valeurs dans \(\mathbb{R}\), \(\pi\)-periodiques.
\(\cos^2(x) + \sin^2(x) = 1\)
\(\tan(x) = \frac{\sin(x)}{\cos(x)}\)
\(\sin(-x) = -\sin(x)\)
\(\cos(-x) =\cos(x)\)
\(\tan(-x) = - \tan(x)\)
\( 1 + \tan^2(x) = \frac{1}{\cos^2(x)}\)
\(\sin(\pi - x) = \sin(x)\)
\(\cos(\pi - x) = - \cos(x)\)
\(\tan(\pi - x) = - \tan(x)\)
\(\sin(\frac{\pi}{2} - x) = \cos(x)\)
\(\cos(\frac{\pi}{2} - x) = \sin(x)\)
\(\tan(\frac{\pi}{2} - x) = \frac{1}{\tan(x)}\)
\(\sin(2x) = 2\sin(x)\cos(x)\)
\(\cos(2x) = \cos^2(x) - \sin^2(x) = 2\cos^2(x) -1 = 1 - 2\sin^2(x)\)
\(\tan(2x) = \frac{2\tan(x)}{1-\tan^2(x)}\)
\(\sin(x) = \frac{2t}{1+t^2}, \mbox{ avec } t=\tan(\frac{x}{2})\)
\(\cos(x) = \frac{1-t^2}{1+t^2} , \mbox{ avec } t=\tan(\frac{x}{2})\)
\(\tan(x) = \frac{2t}{1-t^2} , \mbox{ avec } t=\tan(\frac{x}{2})\)
Conditions pour lesquelles cos(x) est égal à une valeur donnée \(y\) :#
En général, pour une valeur donnée \(y\), \(cos(x) = y\) si \(x = arccos(y) + 2\pi k\) ou \(x = -arccos(y) + 2\pi k\), pour tout entier \(k\).
Remarque spéciale : \(cos(x) = 0\) lorsque \(x = \frac{\pi}{2} + \pi k\), pour tout entier \(k\).
Conditions pour lesquelles sin(x) est égal à une valeur donnée \(y\) :#
En général, pour une valeur donnée \(y\), \(sin(x) = y\) si \(x = arcsin(y) + 2\pi k\) ou \(x = \pi - arcsin(y) + 2\pi k\), pour tout entier \(k\).
Remarque spéciale : \(sin(x) = 0\) lorsque \(x = \pi k\), pour tout entier \(k\).
Conditions pour lesquelles tan(x) est égal à une valeur donnée \(y\) :#
En général, pour une valeur donnée \(y\), \(tan(x) = y\) si \(x = arctan(y) + \pi k\), pour tout entier \(k\).
Remarque spéciale : \(tan(x) = 0\) lorsque \(x = \pi k\), pour tout entier \(k\).
table des valeurs#
Voici une table des valeurs remarquables pour les fonctions sinus (\(\sin\)), cosinus (\(\cos\)) et tangente (\(\tan\))
Angle (x) |
sin(x) |
cos(x) |
tan(x) |
|---|---|---|---|
\(-2\pi\) |
0 |
1 |
0 |
\(-\frac{11\pi}{6}\) |
\(\frac{1}{2}\) |
-\(\frac{\sqrt{3}}{2}\) |
\(\frac{1}{\sqrt{3}}\) |
\(-\frac{7\pi}{4}\) |
\(\frac{\sqrt{2}}{2}\) |
-\(\frac{\sqrt{2}}{2}\) |
-1 |
\(-\frac{5\pi}{3}\) |
\(\frac{\sqrt{3}}{2}\) |
-\(\frac{1}{2}\) |
-\(\sqrt{3}\) |
\(-\frac{3\pi}{2}\) |
-1 |
0 |
Non définie |
\(-\frac{4\pi}{3}\) |
-\(\frac{\sqrt{3}}{2}\) |
-\(\frac{1}{2}\) |
\(\sqrt{3}\) |
\(-\frac{5\pi}{4}\) |
-\(\frac{\sqrt{2}}{2}\) |
-\(\frac{\sqrt{2}}{2}\) |
1 |
\(-\frac{7\pi}{6}\) |
-\(\frac{1}{2}\) |
-\(\frac{\sqrt{3}}{2}\) |
\(\frac{1}{\sqrt{3}}\) |
\(-\pi\) |
0 |
-1 |
0 |
\(-\frac{5\pi}{6}\) |
\(\frac{1}{2}\) |
-\(\frac{\sqrt{3}}{2}\) |
-\(\frac{1}{\sqrt{3}}\) |
\(-\frac{3\pi}{4}\) |
\(\frac{\sqrt{2}}{2}\) |
-\(\frac{\sqrt{2}}{2}\) |
-1 |
\(-\frac{2\pi}{3}\) |
\(\frac{\sqrt{3}}{2}\) |
-\(\frac{1}{2}\) |
-\(\sqrt{3}\) |
\(-\frac{\pi}{2}\) |
1 |
0 |
Non définie |
\(-\frac{\pi}{3}\) |
\(\frac{\sqrt{3}}{2}\) |
\(\frac{1}{2}\) |
\(\sqrt{3}\) |
\(-\frac{\pi}{4}\) |
\(\frac{\sqrt{2}}{2}\) |
\(\frac{\sqrt{2}}{2}\) |
1 |
\(-\frac{\pi}{6}\) |
\(\frac{1}{2}\) |
\(\frac{\sqrt{3}}{2}\) |
\(\frac{1}{\sqrt{3}}\) |
0 |
0 |
1 |
0 |
\(\frac{\pi}{6}\) |
\(\frac{1}{2}\) |
\(\frac{\sqrt{3}}{2}\) |
\(\frac{1}{\sqrt{3}}\) |
\(\frac{\pi}{4}\) |
\(\frac{\sqrt{2}}{2}\) |
\(\frac{\sqrt{2}}{2}\) |
1 |
\(\frac{\pi}{3}\) |
\(\frac{\sqrt{3}}{2}\) |
\(\frac{1}{2}\) |
\(\sqrt{3}\) |
\(\frac{\pi}{2}\) |
1 |
0 |
Non définie |
\(\frac{2\pi}{3}\) |
\(\frac{\sqrt{3}}{2}\) |
-\(\frac{1}{2}\) |
-\(\sqrt{3}\) |
\(\frac{3\pi}{4}\) |
\(\frac{\sqrt{2}}{2}\) |
-\(\frac{\sqrt{2}}{2}\) |
-1 |
\(\frac{5\pi}{6}\) |
\(\frac{1}{2}\) |
-\(\frac{\sqrt{3}}{2}\) |
-\(\frac{1}{\sqrt{3}}\) |
\(\pi\) |
0 |
-1 |
0 |
\(\frac{7\pi}{6}\) |
-\(\frac{1}{2}\) |
-\(\frac{\sqrt{3}}{2}\) |
\(\frac{1}{\sqrt{3}}\) |
\(\frac{5\pi}{4}\) |
-\(\frac{\sqrt{2}}{2}\) |
-\(\frac{\sqrt{2}}{2}\) |
1 |
\(\frac{4\pi}{3}\) |
-\(\frac{\sqrt{3}}{2}\) |
-\(\frac{1}{2}\) |
\(\sqrt{3}\) |
\(\frac{3\pi}{2}\) |
-1 |
0 |
Non définie |
\(\frac{5\pi}{3}\) |
-\(\frac{\sqrt{3}}{2}\) |
\(\frac{1}{2}\) |
-\(\sqrt{3}\) |
\(\frac{7\pi}{4}\) |
-\(\frac{\sqrt{2}}{2}\) |
\(\frac{\sqrt{2}}{2}\) |
-1 |
\(\frac{11\pi}{6}\) |
-\(\frac{1}{2}\) |
\(\frac{\sqrt{3}}{2}\) |
-\(\frac{1}{\sqrt{3}}\) |
\(2\pi\) |
0 |
1 |
0 |
